概念

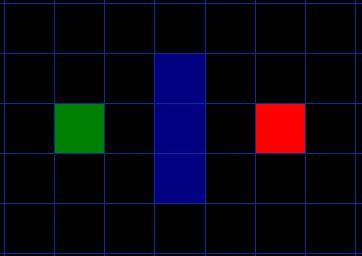
A*寻路算法解决的问题是寻找A点到B点的最短路径，不能碰到障碍，如图中所示，绿色块为出发点A点，红色块为目标B点，蓝色块为障碍。

我们将问题简化为，路径区域为方格网络。因此可以将路径简化为二位数组表示，数组中的每项表示方格，它的值代表它能否走通（即是否障碍）。

另外我们把走路的人，视为站在方格的中心上，一旦找到最短路径时，他是从一个方格的中心走到下一个方格的中心。这些方格中心，称为”节点”。我们就用这些”节点”表示方格。

开始查找

一旦我们将路径简化为二位数组，通过上面讲把路径区域视为方格网络，那么下一步就是要实现搜索最短路径。我们把A点作为开始点，查找它可以联接的点，然后一直往外搜索直到我们的目标点。

1. 首先把A点加入一个待检查的列表”open list”。 “open list”就像一个购物清单。现在它只有一个节点，不过会越来越多，它包含那些你可能或不能走的路径，总之你需要检查的路径。
2. 查找所有的可以联接到开始点的非障碍方格，也把它们加入”open list”。对这些点，将A点保存为它们的父节点，方便我们回溯路径。
3. 将A方格从”open list”移除，加到”closed list”中，”closed list”中保存着不需要再考虑的方格。

现在，我们需要做个说明，以方便后面的讲解。如下图， 中间的深绿色方格是开始方格。它包围着浅蓝色轮廓表示它被加入了”closed list”，所有的联结点现在在”open list”中待检查，它们包围着浅绿的轮廓，不同颜色的轮廓指示了它们在不同的list。每个联结点都有一条灰线指向它的父节点。

下一步，我们选择其中一个”open list”的联结点，然后差不多是重复着上面的步骤。但是我们应该选择哪个节点呢？答案是，最小F值的那个。

路径值

决定选取哪些方格的关键，是要计算出路径的值，就是下面的等式！
F = G + H
其中，

• G —》从出发点到某点的路程，按照前面选取的一条路径
• H —》从给定点到某点的预估路程，因为还没产生某点到终点的路径，所以这个值是一个猜测的。

我们选取路径的方式就是，不断的从”open list”取出节点，然后选择最小F值的方格。随后我们将更详细的讨论这个，先说下我们是怎么计算这个等式的。

如上所述，G值是从开始点到某方格的路程。在这个例子中，我们指定一个水平或垂直的移动为路程10，以及一个对角移动为路程14。我们使用14，而不是10根号2的实际距离 ，是为了方便计算。

开始点沿特定的路径到某方格的G值，等于某方格的父节点的G值加上10或14，这看它是沿父节点方格的对角还是非对角移动的。

H值可用很多方法估算。我们在这里使用曼哈顿方法。具体说，就是计算水平或垂直方向从当前方格移动到目标方格的总方格数目，无视对角运动并忽略了可能碰到的任何障碍。然后，我们将总数乘以10（水平或垂直移动一格的成本）。这被称为曼哈顿方法，大概是因为它像计算城市街区的数量从一个地方到另一个地方，在那里你不能跨块切成斜。

看上面的说明，你可能想这估算法仅仅是当前方格与目标方格的剩余距离的很粗略的估算。我们实际上试图估计沿路径的剩余距离（通常是更远）。我们的估计与实际剩余距离越接近，算法就更快。然后如果我们高估了这个距离，它并不能保证给我们的最短路径。在这种情况下，我们称为”不可接受的估算”。

从技术上讲，在该例子中，曼哈顿方法是不可接受的，因为它稍高估了剩下的距离。但是，我们用用也无妨，因为它只是稍微高估了，而且可以更容易理解我们的目的。在那些所得到的路径不是最短路径的极少情况下，所得路径跟最短路径几乎一样短。想知道更多关于估算方法？可以参阅这里。

F由G加H所得。第一个步搜索路径的结果可以看下面的图示。F，G和H的值写在每个方格上面，F在左上角，G在左下角，H右下角。

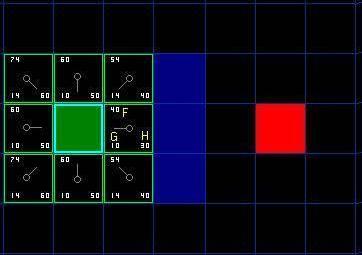
我们可以看到开始点的上下左右方块的G值=10，因为它们是开始点水平或垂直方向移动过去的，而对角的4个方块的G值=14。

H值是由开始点到红色目标块的曼哈顿距离，只是